更新日: 2020/12/17
赤外分光スペクトルは非常に多くの吸収バンドで構成されるため、ピークどうしが重なり合うケースが多くなります。ピークの重なりをどうやって見抜きますか?
前回は、スペクトルを微分することで定量性を保ったまま半値幅を狭めることができる、という特徴を、単一のピークに着目してご説明しました。今回はこの特徴が2つ以上のピークが重なった場合にも適応できるかをはじめに考えます。次にその応用として、ピーク分離とベースライン補正への適用例をご紹介します。
ピーク分離
前回触れたスペクトルの微分の特徴はピークが複数重なっていても適応できます。これは和の微分の公式で理解できます。関数Fと関数Gの和の微分には、下式の関係があります。
【和の微分の公式】
d(F+G)dλ = dFdλ + dGdλ
ここで関数 F が 1 つ目のピーク、関数 G が 2 つ目のピークと考えます。するとこの式は、F と G が重なりあったピークを微分することは、それぞれのピークを微分して和を取ることに等しい、という意味になります。図で表すと以下のようになります。データは前回のものと同様シミュレーション値です。
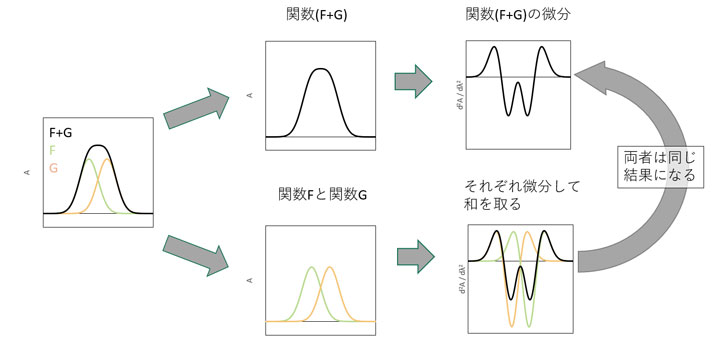
図1 重なり合うスペクトルの分離
図の上段側は、重なり合ったピークを微分した場合、図の下段側は、それらの個々のスペクトルを微分した後に足し合わせた場合です。どちらも最終的に同じ微分スペクトルが得られていることがわかります。
また、2 次微分を取ることで個々のピークの半値幅が狭まり、それぞれのピークトップの位置が明確になることがわかります。
実際のスペクトルで試してみましょう。図は市販の PET ボトルの ATR スペクトルです。分解能 2 cm-1 で測定しています。(分解能についてはこちらをご覧ください。) 3 つのスペクトルは、それぞれ飲料メーカーが異なるものです。スペクトルのうち 1720 cm-1 付近の C=O 伸縮振動を拡大表示しました。
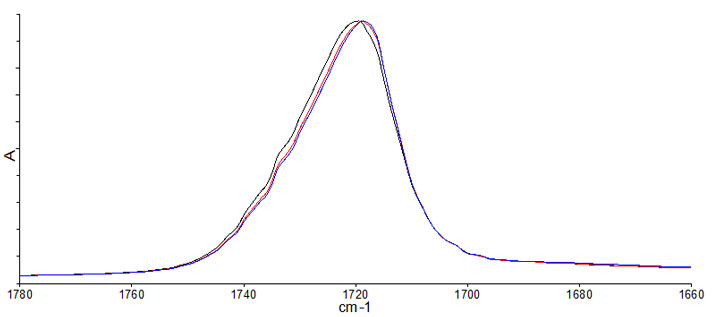
図2 市販PETボトルのATRスペクトル
一見 1 つのピークのように見え、3 つのスペクトルの間で違いがあるようには見えません。しかし微分してみると違って見えます。
Spectrum IR ソフトウェアで微分処理を実行する場合、は、処理メニュー → 微分を選んでください。または、  のアイコンをクリックしてください。処理画面では微分の次数とフィルタの範囲を選択できます。今回は 4 次微分を実行しました。結果は以下のようになります。
のアイコンをクリックしてください。処理画面では微分の次数とフィルタの範囲を選択できます。今回は 4 次微分を実行しました。結果は以下のようになります。
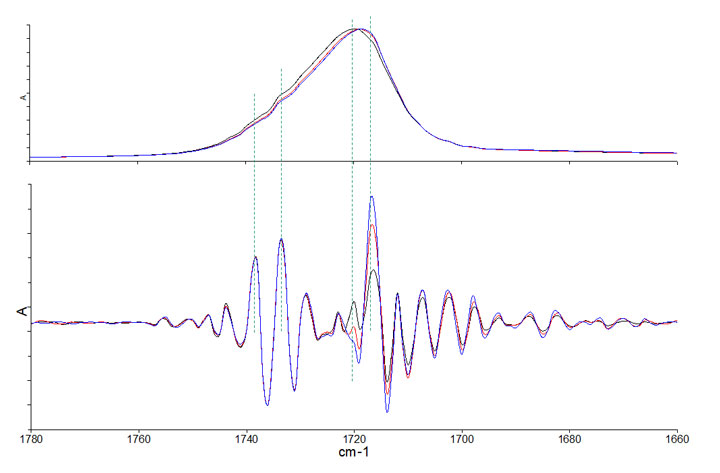
図3 微分の処理画面
単一のように見えたピークが複数のピークに分離できていることがわかります。特に、1720 cm-1 (芳香族エステル基)のピークが 2 本に分離しており、飲料メーカーごとに異なっていることがわかります。さらに 1740, 1730 cm-1 付近に脂肪族エステル基と考えられるピークの存在が示唆されます。
このように、微分によりピークを分離し、隠れたピークの存在を浮き上がらせることができます。
ただし、繰り返しになりますが、上記のような高次の微分スペクトルでは、常にサイドローブによる偽ピークに常に気を付ける必要がある点は注意しなければなりません。
微分のアルゴリズム:Savitzky-Golay法
Spectrum IR の微分のアルゴリズムにはサビツキーゴーレイ法 (Savitzky-Golay法, SG法) 1) が使われています。デジタルデータを微分したりスムージングしたりする際に最も多く利用される方法です。
あまり知られていませんが、この Savitzky-Golay 法は、1964 年に米国パーキンエルマーの A . Savitzky 氏と M.J.E. Golay 氏によって発表された方法なのです。赤外分光分析以外のデータ解析にも適用できるため、今では極めて広範囲な用途で使われています。その論文1)は分析化学分野で権威のある学術雑誌 Analytical Chemistry 誌で “最も引用された論文の一つ” として知られています。
Savitzky-Golay 法については、また別の機会にご紹介します。
ベースライン補正
さて、ここからは微分のもう一つの用途、ベースライン補正についてご説明します。
ベースライン補正も、和の微分の公式の特徴を考えると理解しやすくなります。
この場合、スペクトルがピーク(関数F)とベースライン(関数B)の和でできていると考えます。
d(F+B)dλ = dFdλ + dBdλ
ベースラインの関数 B は 1 次関数や 2 次関数など低次の多項式で近似できます。ベースラインの傾きはピーク高さの傾きに対して十分小さいからです。
もしベースラインが 2 次関数で近似できるなら、1 次微分を取るとベースラインの傾きは直線になります。さらに 2 次微分を取るとベースラインの項にはごく小さな値の定数が残るだけ、となります。
シミュレーションでも、F にベースラインを加えて計算した関数 (F+B) が、その微分により関数Fの形状に近づいており、ベースラインを良好に補正できていることがわかります。
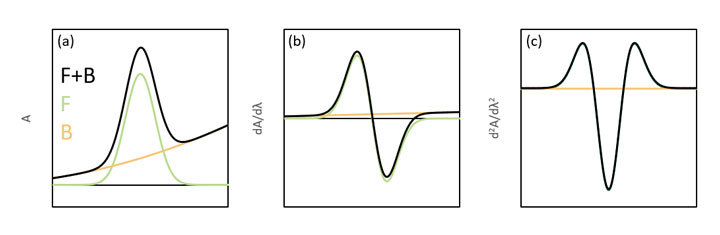
図4 ベースライン補正
生データ (a), 1次微分 (b)、2次微分 (c)
ベースライン補正も実際のスペクトルで試してみましょう。PET 樹脂を熱と紫外線で極端に劣化させ、サンプルとして使用しました。実験の都合上、分解能の条件が図 2 のものと異なります。このような劣化サンプルの測定では赤外光の散乱状態がスペクトル毎に異なるため、ベースラインが大きく変動することがあります。
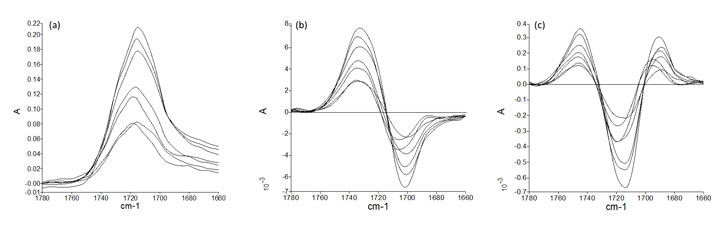
図5 PETのC=O伸縮振動ピークの微分によるベースライン補正
生データ (a), 一次微分 (b), 二次微分 (c)
生データではピークの裾のベースラインの傾きと変動が大きくなっています。1 次微分を取ることでベースラインが補正され、ベースラインの変動が抑制されていることがわかります。さらに 2 次微分を取ると、ベースラインの値がさらに 0 に近づきます。
このような微分を用いたベースライン補正は、多変量解析 (PCA)や多変量解析を用いた定量分析(たとえば PCR や PLS)の前処理として、頻繁に利用されています。ベースラインが補正されることで、モデルを構築するための主成分(ファクター)の数を減らせるメリットがあります。結果としてベースライン変動に由来するデータのばらつきを抑えることができます。
まとめ
スペクトルを微分することでピークを分離したりベースラインを補正したりすることができることをご説明しました。
さらに微分スペクトルには定量性が保たれています。
次回は、微分スペクトルの定量について書きます!
参考文献
1) Savitzky. A, Golay. M.J.E, Analytical Chemistry 36, (8), 1627–39, (1964).
☆以下のエントリも参考になりますので、併せてご覧ください☆