更新日: 2020/12/8
データの中の小さな変化に気付ける。機器分析での測定・解析に携わる多くの人にとって大事なスキルです。特に赤外分光スペクトルは非常に多くの吸収バンドで構成されるため、ピークどうしが重なり合うケースが多くなります。大きなピークの肩に小さなピークがあるかどうか、皆さんはどうやって見抜くでしょうか?
そのような時、ピーク分離処理により隠れたピークを浮き上がらせることができます。ピーク分離にはいくつかの方法がありますが、代表的なものは
- スペクトルの微分
- フーリエセルフデコンボリューション
の 2 つです。今回はこれらの方法のうちスペクトルの微分にフォーカスを当ててお話します。
スペクトルの微分をすると良いことがあるの?
①ベースラインを平坦にする
②ピークの半値幅を狭めて、大きいピークのそばにある識別しにくい小さなピークの位置を明確にする
ことで、定量分析の正確さを上げることができます。
今回から 3 回に渡り、スペクトルの微分をテーマにお話ししていきます。でも微分と聞くと、なんだか難しそうだな・・・と思われる方も多いと思いますので、できる限り丁寧に説明していきます。
今回は、微分スペクトルでできることと、そもそも微分って何よ?と言うための方に、数学的な観点から微分の意味を簡単におさらいし、ピークを微分することのイメージをお伝えします。
2 回目は、微分の特徴を上手く活用し、ベースラインを補正する方法や複雑なピークのピーク分離をする方法など、微分をスペクトル解析にどう活かすかをご説明します。
3回目は、定量する際の条件の決め方をもとに、実際に微分スペクトルによる定量を実践してみます。
では早速始めましょう!
微分って何?
さて、微分って何??という人も多いかと思いますので、スペクトルの解析に使うところだけに限定して、簡単におさらいしておきましょう。中学校の数学〜高校の数Ⅱあたりまでの内容です。
プログの初回で、数式は使いません、とお約束しましたが、、スミマセン!ここだけは使ったほうがわかりやすいので数式で表現させていただきます。
微分するとは、直感的に言うと傾きを取ることです。例えば、
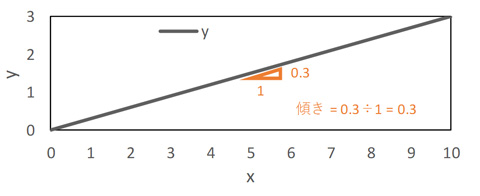
図1 微分とは傾きを取ること
直線の関数 y = 0.3x を微分してみましょう。この関数の傾きは、x のどの地点でも 0.3 です。なので関数 y の 1 次微分 y’ は 0.3 となります。
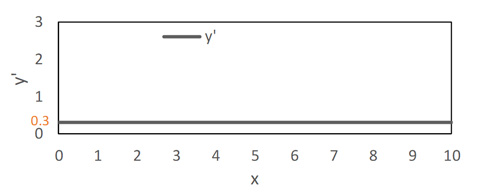
図2 y = 0.3xの1次微分。y’ = 0.3
一般的に、y = ax + b のとき、y’ = a となります。
多くの関数は曲線でできています。例えば 2 次関数。
曲線でできている関数は x の各地点での傾きが変わります。そんな時は、各点での曲線の接戦から傾きを求めます。
関数 y = 0.03x2 を微分すると、y’= 0.06x となります。
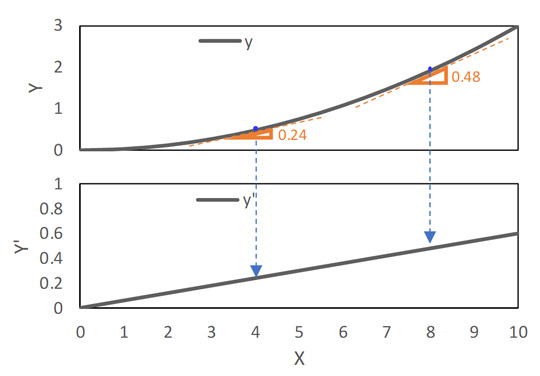
図3 y = 0.03x2 の微分。y' = 0.06x
一般的には、y = ax2 + bx + c のとき、 y' = 2ax + b となります。
1 次微分をさらに微分することもできます。2 回微分することを 2 次微分、3 回微分することを3次微分と呼びます。2 次微分は y''、3 次微分は y''' と表現します。
スペクトルの解析で使われるのはほとんどの場合 1 次微分か 2 次微分です。まれに 3 次、4 次微分が使われることもあります。5 次微分以上はめったにお目にかかることはありません。
ピークを微分してみる
さて、IR スペクトルのある 1 つのピークも曲線でできた関数なので、微分できます。スペクトルやピークを関数で示す時は横軸が波数 λ、縦軸が吸光度 A となるので、グラフの表現も横軸 x の代わりにλ、縦軸 y の代わりに A を使うことにします。
関数 A の 1 次微分の表現もA'の代わりに dAdλ としましょう。2 次微分は d2Adλ2 、4 次微分は d4Adλ4 です。
微分の次数を明確にするため、縦軸にこのような表現が使われることがあります。
ピークを 1 次〜 4 次微分すると次のようになります。
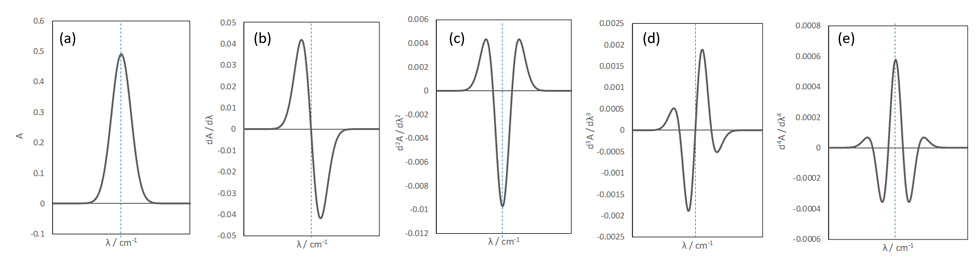
図4 ピークのシミュレーションデータ。生データ(a)、1次微分(b)、2次微分(c)、3次微分(d)、4次微分(e)。
図 4(b) のようにスペクトルを 1 次微分すると、生データのピークトップが 0 点と交わります。この交点をゼロクロシングポイントと呼びます。一般的に奇数次微分の場合、ピークトップがゼロ点と交わります。そのため、ピークトップの位置を決定するために 1 次微分のゼロクロシングポイントを検出するアルゴリズムが使われることがあります。1 次微分の極大値と極小値は、元のピークの変曲点になります。
2 次微分の場合、生データと似たような左右対称の波形が得られますが、ピークが下に凸になります。ですので、ピークの定量値は負の数となります。定量値を正の数にするため、縦軸にマイナスを掛け合わせて - d2Adλ2 とすることがあります。2 次微分スペクトルでは生データより半値幅が狭くなり、バンドの形状がシャープになっていることがわかります。
4 次微分では再び上に凸のピークが現れます。半値幅は 2 次微分スペクトルよりさらに狭くなり、ピークが非常に鋭くなっています。微分の次数が増えると、生データのピークの裾に擬ピークが出現するため、スペクトルの解釈が複雑になってきます。擬のピークを真のピークと間違えないように注意する必要があります。
微分スペクトルの定量性
微分するとピークの形状は変形しますが、ピーク高さの関係は保たれるのでしょうか。
保たれます。数学的な取り扱いは文献 1,2) に譲るとして、ここでは直感的にグラフで示しました。生データ、1 次微分、2 次微分、4 次微分のピーク高さの関係を示しました。
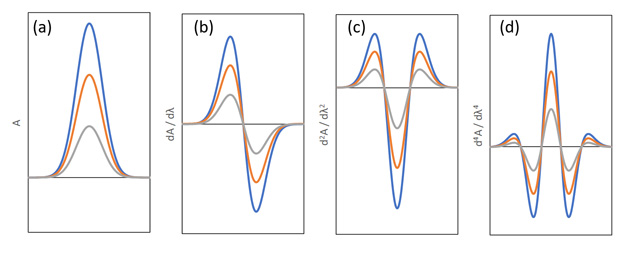
図5 強度の異なるピークのシミュレーションデータ。
基準スペクトル(灰) 基準の2倍強度(オレンジ)、基準の3倍強度(青)。
生データ(a), 1次微分(b), 2次微分(c), 4次微分(d)。
微分してもピーク強度の関係は変わらないことがわかります。生データを微分しても定量性は保たれます。そのため、スペクトルの微分は解析では古くからよく利用されるのです2)。
まとめ
基礎編ではある単一のピークに着目し、微分スペクトルを微分しても定量性が保たれることを説明しました。
次回は複雑なピークのピーク位置を明確にする方法や、変動するベースラインを補正する方法など、微分をスペクトル解析にどう活かすかをご説明します。
参考文献
1) G. Talsky, L. Mayring, and H. Kreuzer, Angew. Chem., Int. Ed. m., 11, 785 (1978)
2) Dixit L, Ram. S, Applied Spectroscopy Reviews, 21, (4), 311–418 (1985)
☆以下のエントリも参考になりますので、併せてご覧ください☆